Analytic Geometry Assignment No.2

1. 一个直三棱柱体，如下图所示，其中 $\overline{AB}\perp\overline{AC}$ ， $E$ 是 $\overline{AC}$ 的中点， $F$ 是 $\overline{A_1B_1}$ 的中点。已知 $|\overline{AB}| = |\overline{AC}| = 4$ ， $|\overline{AA_1}| = 6$ 。求 $\overline{EF}$ 与 $\overline{A_1C}$ 的夹角与距离.

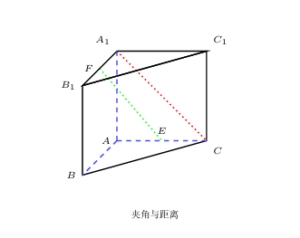
以 $\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|},\frac{\overrightarrow{AA_1}}{|\overrightarrow{AA_1}|},\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$ 为标准右手直角坐标系,则 $\overrightarrow{EF}=(-2,6,2)$ , $\overrightarrow{A_1C}=(4,-6,0)$ , $\overrightarrow{EA_1}=(-2,6,0)$ ,则 $\operatorname{Arg}(\overline{EF},\overline{A_1C})=\arccos(\frac{|\overrightarrow{EF}\cdot\overrightarrow{A_1C}|}{|\overline{EF}|\cdot|\overline{A_1C}|})=\arccos\frac{|-8-36|}{2\sqrt{11}\cdot2\sqrt{13}}=\arccos\frac{\sqrt{11}}{\sqrt{13}}$ , $d(\overline{EF},\overline{A_1C})=\frac{|(\overrightarrow{EA_1},\overrightarrow{EF},\overrightarrow{A_1C})|}{|\overrightarrow{EF}\times\overrightarrow{A_1C}|}=\frac{|-24+48|}{4\sqrt{22}}=\frac{6}{\sqrt{22}}$ .

2. 一个长方体，如下图所示，已知 $|\overline{AB}|=3$ ， $|\overline{AD}|=4$ ， $|\overline{AA_1}|=7$ ， $|\overline{BM}|=2$ 。求三角形 $A_1MC$ 的面积，以及点 $A$ 到三角形 $A_1MC$ 的距离.

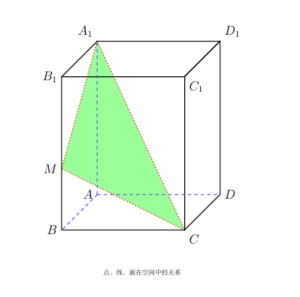
以 $\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|},\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|},\frac{\overrightarrow{BB_1}}{|\overrightarrow{BB_1}|}$ 为标准右手直角坐标系,则 $\overrightarrow{MC}=(4,0,-2)$ , $\overrightarrow{MA_1}=(0,3,5)$ , $\overrightarrow{MA}=(0,3,-2)$ ,则 $S_{A_1MC}=\frac{|\overrightarrow{MC}\times\overrightarrow{MA_1}|}{2}=\sqrt{145}$ , $d(A,A_1MC)=\frac{|\overrightarrow{MA}\cdot(\overrightarrow{MC}\times\overrightarrow{MA_1})|}{|\overrightarrow{MC}\times\overrightarrow{MA_1}|}=\frac{|-60-24|}{2\sqrt{145}}=\frac{42}{\sqrt{145}}$ .

3. 讨论轮子上一条固定半径的中点A的运动状态，并求运动轨迹.

设圆心 $O$ ,初始圆心 $O_0$ ,以 $\{O;\vec i,\vec j\}$ 为标架, $A$ 点在此标架下的参数轨迹为 $A(\frac{r}{2}\cos\theta,\frac{r}{2}\sin\theta)$ ,考虑圆心 $O$ 有 $\overrightarrow{O_0O}=(-r\theta,0)$ ,所以 $(x,y)\mapsto(x-r\theta,y)$ 为 $\{O;\vec i,\vec j\}$ 到 $\{O_0;\vec i,\vec j\}$ 的变换,在此变换下轨迹变为 $A(\frac{r}{2}\cos\theta-r\theta,\frac{r}{2}\sin\theta)$ ,即为所求.

4. (内摆轮线) 有一个固定的轮子，半径为 $R$ . 另有一个半径为 $r$ ( $r<R$ )的轮子，沿着固定轮子的内边缘纯粹滚动(无滑动)。求小轮子边缘上一个固定点 $A$ 的运动轨迹.

设外轮圆心 $O(0, 0)$ ,内轮圆心 $P$ ,内轮初始圆心 $P_0((R-r)\cos\theta_0,(R-r)\sin\theta_0)$ ,以 $\{P;\vec i,\vec j\}$ 为标架,不妨设 $A$ 点在此标架下的参数轨迹为 $A(r\cos\theta,r\sin\theta)$ ,考虑内轮圆心 $P$ 有 $\overrightarrow{OP}=(R-r)\begin{bmatrix}\cos(\theta_0-\frac{r}{R-r}\theta)\\\sin(\theta_0-\frac{r}{R-r}\theta)\end{bmatrix}$ ,所以 $(x,y)\mapsto(x,y)+\overrightarrow{OP}$ 为 $\{P;\vec i,\vec j\}$ 到 $\{O;\vec i,\vec j\}$ 的变换,在此变换下轨迹变为 $A(r\cos\theta+(R-r)\cos(\theta_0-\frac{r}{R-r}\theta),r\sin\theta+(R-r)\sin(\theta_0-\frac{r}{R-r}\theta))$ ,即为所求.

5. (外摆轮线) 有一个固定的轮子，半径为 $R$ 。另有一个半径为 $r$ 的轮子，沿着固定轮子的外边缘纯粹滚动(无滑动)。求小轮子边缘上一个固定点 $A$ 的运动轨迹.

设外轮圆心 $O(0, 0)$ ,外轮圆心 $P$ ,外轮初始圆心 $P_0((R+r)\cos\theta_0,(R+r)\sin\theta_0)$ ,以 $\{P;\vec i,\vec j\}$ 为标架,不妨设 $A$ 点在此标架下的参数轨迹为 $A(r\cos\theta,r\sin\theta)$ ,考虑内轮圆心 $P$ 有 $\overrightarrow{OP}=(R+r)\begin{bmatrix}\cos(\theta_0+\frac{r}{R+r}\theta)\\\sin(\theta_0+\frac{r}{R+r}\theta)\end{bmatrix}$ ,所以 $(x,y)\mapsto(x,y)+\overrightarrow{OP}$ 为 $\{P;\vec i,\vec j\}$ 到 $\{O;\vec i,\vec j\}$ 的变换,在此变换下轨迹变为 $A(r\cos\omega t+(R+r)\cos(\theta_0+\frac{r}{R+r}\theta),r\sin\omega t+(R+r)\sin(\theta_0+\frac{r}{R+r}\theta))$ ,即为所求.

6. 证明曲线 $r(t)$ 是球面曲线当且仅当 $r\cdot r' \equiv0$ .

$r(t)$ 是球面曲线 $\Leftrightarrow$ $\exist R\ni |r|^2=R^2$ $\Leftrightarrow$ $(|r|^2)'=2r\cdot r'\equiv0$ $\Leftrightarrow$ $r\cdot r'\equiv 0$ .

7. 设粒子的运动轨迹为 $r(t) =\begin{bmatrix}a\cos t\\a\sin t\\bt^2\end{bmatrix}$ ，其中 $ab\neq0$ . 求粒子的运动速度以及粒子从时刻 $t=0$ 到 $t=\pi$ 时刻的运动距离，并求曲率与挠率.

$v=r'=\begin{bmatrix}-a\sin t\\a\cos t\\2bt\end{bmatrix}$ , $s=\int_0^\pi |v|\mathrm{d}t=\int_0^\pi\sqrt{a^2+4b^2t^2}\mathrm{d}t=\frac{a^2}{2b}(\frac{\frac{2b}{a}\sqrt{\frac{4b^2}{a^2}+1}+\ln(\sqrt{\frac{4b^2}{a^2}+1}+\frac{2b}{a})}{2})=\frac{\sqrt{a^2+4b^2}}{2}+\frac{a^2}{4b}(\ln(\sqrt{a^2+4b^2}+2b)-\ln a)$ , $r''=\begin{bmatrix}-a\cos t\\-a\sin t\\2b\end{bmatrix},r'\times r''=\begin{bmatrix}2ab\cos t+2abt\sin t\\2ab\sin t-2abt\cos t\\a^2\end{bmatrix},|r'\times r''|=a\sqrt{a^2+4b^2(t^2+1)},\mathfrak k=\frac{|r'\times r''|}{|r'|^3}=\frac{a\sqrt{a^2+4b^2(t^2+1)}}{(\sqrt{a^2+4b^2t^2})^3},r'''=\begin{bmatrix}a\sin t\\-a\cos t\\0\end{bmatrix},(r',r'',r''')=2a^2bt,\tau=\frac{(r',r'',r''')}{|r'\times r''|^2}=\frac{2bt}{a^2+4b^2(t^2+1)}$ .

P. 设有一艘飞船其轨迹为 $\vec r(t)=(3+t)\vec i+(2+\ln t)\vec j+(7-\frac{4}{t^2+1})\vec k$ . 设空间站的位置为 $(6,4,9)$ .

(1) 若船长想要在空间站停泊，他应该在何时关掉引擎？

$\vec r'=\vec i+\frac{1}{t}\vec j+\frac{8t}{(t^2+1)^2}\vec k$ . $((6,4,9)-\vec r)\times \vec r'=0\Rightarrow(\frac{8t(2-\ln t)}{(t^2+1)^2}-\frac{1}{t}(2+\frac{4}{t^2+1}),\frac{8t(t-3)}{(t^2+1)^2}+2+\frac{4}{t^2+1},\frac{3-t}{t}-2+\ln t)=0\Rightarrow t=1$ . 所以在 $t=1$ 时.

(2) 关掉引擎时刻曲线的曲率与挠率.

$\vec r''=-\frac{1}{t^2}\vec j-\frac{32t^2}{(t^2+1)^3}\vec k,\vec r'''=\frac{2}{t^3}\vec j+\frac{192t^3}{(t^2+1)^4},\vec r'(1)=(1,1,2),\vec r''(1)=(0,-1,-4),\vec r'''(1)=(0,2,12),(\vec r'\times \vec r'')(1)=(-2,4,-1),(\vec r',\vec r'',\vec r''')(1)=-4,\mathfrak k=\frac{\sqrt{21}}{6\sqrt6},\tau=-\frac{4}{21}$ .

(3) 关掉引擎时刻相应的活动标架.

$\vec r(1)=(4,2,5),\mathrm{T}=\frac{1}{\sqrt6}(1,1,2),\mathrm{N}=\frac{1}{\sqrt{14}}(3,1,-2),\mathrm B=\frac{1}{\sqrt{21}}(-2,4,-1)$ ,则 $\{\vec r(1);\mathrm T,\mathrm N,\mathrm B\}$ 即为所求.

8. 设粒子的运动轨迹为 $r(t) =\begin{bmatrix}a\cos t\\ a\sin t\\bt\end{bmatrix}$ ，其中 $ab\neq0$ 。求粒子轨迹的正交活动标架及相应的Frenet-Serret公式.

$r'=(-a\sin t,a\cos t,b),r''=(-a\cos t,-a\sin t,0),r'''=(a\sin t,-a\cos t,0),r'\times r''=(ab\sin t,-ab\cos t,a^2),(r',r'',r''')=a^2b,\mathrm T=\frac{1}{\sqrt{a^2+b^2}}(-a\sin t,a\cos t,b),\mathrm N=(-\cos t,-\sin t,0),\mathrm B=\frac{1}{\sqrt{a^2+b^2}}(b\sin t,-b\cos t,a),\kappa=\frac{a}{a^2+b^2},\tau=\frac{b}{a^2+b^2}$ ,因此 $\{(r;\mathrm T,\mathrm N,\mathrm B):t\in\R\}$ 与 $\begin{bmatrix}\mathrm T'\\\mathrm N'\\\mathrm B'\end{bmatrix}=\frac{1}{\sqrt{a^2+b^2}}\begin{bmatrix}0&a&0\\-a&0&b\\0&-b&0\end{bmatrix}\begin{bmatrix}\mathrm T\\\mathrm N\\\mathrm B\end{bmatrix}$ 即为所求.

9. 设曲面 $S$ 由如下方式给出: $\left\{\begin{matrix} x =r\cos\theta \\ y =r\sin\theta \\ z =b\theta\end{matrix}\right.$ $(0\leq r \leq1, 0\leq\theta \leq2\pi, b>0)$ ，求曲面在一点处的面积元，及该点处的 $D_P$ ， $M_P$ ，以及该点处的法曲率 $\mathfrak{k_n}$ .

$S_r=(\cos\theta,\sin\theta,0),S_\theta=(-r\sin\theta,r\cos\theta,b),S_r\times S_\theta=(b\sin\theta,-b\cos\theta,r),\mathrm{n} =\frac{1}{\sqrt{b^2+r^2}}(b\sin\theta,-b\cos\theta,r),S_{rr}=0,S_{r\theta}=S_{\theta r}=(-\sin\theta,\cos\theta,0),S_{\theta\theta}=(-r\cos\theta,-r\sin\theta,0)$ ,因此 $\mathrm dS=|S_r\times S_\theta|\mathrm dr\mathrm d\theta=\sqrt{b^2+r^2}\mathrm dr\mathrm d\theta$ , $D_P=\mathrm dr^2+(r^2+b^2)\mathrm d\theta^2$ , $M_P=-\frac{2b}{\sqrt{b^2+r^2}}\mathrm dr\mathrm d\theta$ , $\mathfrak{k_n}=\frac{-\frac{2b}{\sqrt{b^2+r^2}}\mathrm dr\mathrm d\theta}{\mathrm dr^2+(r^2+b^2)\mathrm d\theta^2}$ .

10. 设曲面 $S$ 满足方程 $z =x^2+y^2$ 。求曲面在 $P(1,1,2)$ 处的面积元，以及该点处的法曲率.

$S_x=(1,0,2x),S_y=(0,1,2y),S_x(P)=(1,0,2),S_y(P)=(0,1,2),(S_x\times S_y)(P)=(-2,-2,1),\mathrm{n}=\frac{1}{3}(-2,-2,1),S_{xx}=(0,0,2),S_{xy}=S_{yx}=0,S_{yy}=(0,0,2),D_P(P)=5\mathrm dx^2+8\mathrm dx\mathrm dy+5\mathrm dy^2,M_P(P)=\frac{2}{3}\mathrm dx^2+\frac{2}{3}\mathrm dy^2$ ,因此 $\mathrm dS|_P=|(S_x\times S_y)(P)|\mathrm dx\mathrm dy=3\mathrm dx\mathrm dy,\mathfrak{k_n}(P)=\frac{\frac{2}{3}\mathrm dx^2+\frac{2}{3}\mathrm dy^2}{5\mathrm dx^2+8\mathrm dx\mathrm dy+5\mathrm dy^2}$ .

11. 设曲面 $S$ 满足方程 $z=x^2-y^2$ 。求曲面在 $P(1,1,0)$ 处的面积元， $D_P$ ， $M_P$ ，以及该点处的法曲率.

$S_x=(1,0,2x),S_y=(0,1,-2y),S_x(P)=(1,0,2),S_y(P)=(0,1,-2),(S_x\times S_y)(P)=(-2,2,1),\mathrm{n}=\frac{1}{3}(-2,2,1),S_{xx}=(0,0,2),S_{xy}=S_{yx}=0,S_{yy}=(0,0,-2)$ ,因此 $\mathrm dS|_P=|(S_x\times S_y)(P)|\mathrm dx\mathrm dy=3\mathrm dx\mathrm dy$ , $D_P(P)=5\mathrm dx^2-8\mathrm dx\mathrm dy+5\mathrm dy^2,M_P(P)=\frac{2}{3}\mathrm dx^2-\frac{2}{3}\mathrm dy^2$ , $\mathfrak{k_n}(P)=\frac{\frac{2}{3}\mathrm dx^2-\frac{2}{3}\mathrm dy^2}{5\mathrm dx^2-8\mathrm dx\mathrm dy+5\mathrm dy^2}$ .