Problem 1
Convert the following linear programming model into standard form and write the final solution.
1. Traveling Salesman Problem
- A traveling salesman needs to visit 5 different cities: A, B, C, D and E. The salesman must start from one city, visit each city exactly once, and then return to the starting city.
The distances between the cities (in kilometers) are given in the table below. Please help the salesman find the shortest possible route.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 10 | 15 | 20 | 25 |
| B | 10 | 0 | 35 | 25 | 30 |
| C | 15 | 35 | 0 | 30 | 15 |
| D | 20 | 25 | 30 | 0 | 20 |
| E | 25 | 30 | 15 | 20 | 0 |
- Considering the table as a matrix $C$, we can write the model as
$$
\min\sum_{i=1}^5\sum_{j\neq i,j=1}^5 C_{ij}x_{ij}\\
\mathrm{s.t.}
\left\{\begin{matrix}
\sum_{i=1,i\neq j}^5 x_{ij}=1,\enspace j=1,\dots,5\\
\sum_{j=1,j\neq i}^5x_{ij}=1,\enspace i=1,\dots,5\\
\sum_{i\in Q}\sum_{j\neq i,j\in Q}x_{ij}+s_Q=|Q|-1, \enspace Q\subsetneq\{1,\dots,5\},|Q|\ge2\\
x_{ij}\in\{0,1\},\enspace i,j=1,\dots,5;s_Q\ge0
\end{matrix}\right.
$$
- By matlab, we know the shortest possible route is $A\rightarrow C\rightarrow E\rightarrow D\rightarrow B\rightarrow A$, with the total distance $85$km.
2. Optimal Material Usage Problem
A car requires one shaft each of type A, B, and C, with specifications of 1.5m, 1m, and 0.7m, respectively. These shafts must be made from the same round steel, which has a length of 4m. Now, 1000 cars need to be manufactured. What is the minimum mount of round steel required to produce these shafts?
- Consider we have $N$ different ways to devide the steel. Consider a matrix $A_{3\times N}$, which cals means ways and rows means how many specific types can get in this way. Let $x_{i}$ stands for the mount of the $i\mathrm{st}$ way. Now we can write the model as
$$
\min\sum_{i=1}^{N}x_i\\
\mathrm{s.t.}
\left\{\begin{matrix}
\sum_{i=1}^{N}x_iA_{ji}-s_j=1000,\enspace j=1,2,3\\
x_i\in \mathbb{Z}^+,\enspace i=1,\dots,N;s_j\ge0,\enspace j=1,2,3
\end{matrix}\right.
$$
- By matlab, we know the minimum mount of round steel required is $813$.
Problem 2
Convert the following linear programming models to standard form.
1.
$$
\min z =-5x_1-6x_2-7x_3 \\
\mathrm{s.t.}
\left\{\begin{matrix}
-x_1-5x_2-3x_3\ge 15 \\
-5x_1-6x_2+10x_3\leq 20 \\
x_1-x_2-x_3=-5 \\
x_1\leq0,x_2\ge0,x_3\enspace\mathrm{unrestricted}
\end{matrix}\right.
$$
- Let $x_1=-x'_1$, $x_3=-x'_1-x_2+5$ and add slack and surplus variables, we have:
$$
\min z =12x_1'+x_2-35 \\
\mathrm{s.t.}
\left\{\begin{matrix}
4x_1'-2x_2-s_1=30 \\
-5x'_1-16x'_2+s_2= -30 \\
x'_1,x_2,s_1,s_2\ge0
\end{matrix}\right.
$$
2.
$$
\min z =2x_1+5x_2-7x_3 \\
\mathrm{s.t.}
\left\{\begin{matrix}
x_1-2x_2+3x_3\leq-5 \\
2x_1+6x_2-x_3\ge3 \\
3x_1-8x_2+9x_3=6 \\
6x_1-7x_2-4x_3\leq2 \\
x_1\ge0,x_2\leq0,x_3\enspace\mathrm{unrestricted}
\end{matrix}\right.
$$
- Let $x_2=-x_2'$, $x_3=-\frac{1}{3}x_1-\frac{8}{9}x_2'+\frac{2}{3}$ and add slack and surplus variables, we have:
$$
\min z =\frac{13}{3}x_1+\frac{11}{9}x'_2-\frac{14}{3} \\
\mathrm{s.t.}
\left\{\begin{matrix}
-2x_2'+s_1=-21\\
21x_1-46x_2'-s_2=33\\
66x_1+95x_2'+s_3=42\\
x_1,x'_2,s_1,s_2,s_3\ge0
\end{matrix}\right.
$$
Problem 3
Use the graphical method to solve the following linear programming problems, and indicate the nature of the solutions (unique optimal solution, multiple optimal solutions, unbounded solution, or infeasibility).
1.
$$
\max z =2x_1+3x_2 \\
\mathrm{s.t.}
\left\{\begin{matrix}
x_1+2x_2\leq8 \\
x_1+x_2\ge1 \\
x_2\leq4 \\
x_1,x_2\ge0
\end{matrix}\right.
$$
- Drawing the graph in Geogebra, we get:
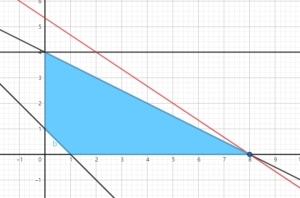
- So the $\max z=16$, when $x_1=8,x_2=0$, which is an unique optimal solution.
2.
$$
\max z =x_1+2x_2 \\
\mathrm{s.t.}
\left\{\begin{matrix}
2x_1+4x_2\leq8 \\
x_1\leq4 \\
x_2\leq3 \\
x_1,x_2\ge0
\end{matrix}\right.
$$
- Drawing the graph in Geogebra, we get:
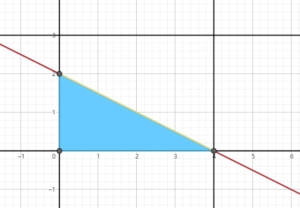
- So the $\max z=4$, when $x_1=4-2x_2,x_2\in[0,2]$, which are multiple optimal solutions.




Comments NOTHING