1. 给出位于第一象限,与正x-轴夹角为\frac{\pi}{3},且长度为4的向量.
- 此向量\vec{v}=\operatorname{Proj}_x\vec v+\operatorname{Proj}_y\vec v=4\cos\frac{\pi}{3}\cdot(1,0)+4\sin\frac{\pi}{3}\cdot(0,1)=(2,2\sqrt3).
2. 求平行于向量8i−j+4k,长度为1的向量. [这样的向量称为单位向量].
- 设向量\vec{v}=\lambda(8i-j+4k),|\vec v|=|\lambda|\sqrt{8^2+(-1)^2+4^2}=1\Rightarrow\lambda=\pm\frac{1}{9},\vec v=\pm(\frac{8}{9}i-\frac{1}{9}j+\frac{4}{9}k)即为所求.
3. 如下图,一个100-kg的物体悬挂在两根绳子上,求两根绳子上的张力 T_1及T_2,并求出力的大小.
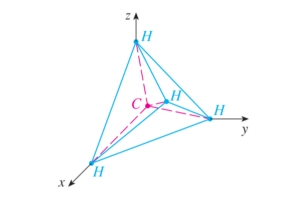
- 根据题意有T_1+T_2+G=0,T_1=-\cos50^\circ|T_1|i+\sin50^\circ|T_1|j,T_2=\cos32^\circ|T_2|i+\sin32^\circ|T_2|j,G=-100\mathrm{g}\cdot j,联立得力的大小|T_1|=\frac{100}{\sin50^\circ+\sin32^\circ\frac{\cos50^\circ}{\cos32^\circ}}\mathrm{g}=\frac{\cos32^\circ}{\sin82^\circ}\cdot100\mathrm{g}牛顿,|T_2|=\frac{\cos50^\circ}{\cos32^\circ}|T_1|=\frac{\cos50^\circ}{\sin82^\circ}\cdot100\mathrm{g}牛顿,因此T_1=-\frac{100\cos50^\circ\cos32^\circ}{\sin82^\circ}\mathrm{g}\cdot i+\frac{100\sin50^\circ\cos32^\circ}{\sin82^\circ}\mathrm{g}\cdot j,T_2=\frac{100\cos32^\circ\cos50^\circ}{\sin82^\circ}\mathrm{g}\cdot i+\frac{100\sin32^\circ\cos50^\circ}{\sin82^\circ}\mathrm{g}\cdot j.
4. 如图,绳子两端的张力T大小为25N,则绳子重量是多少.

- 根据题意有T_1+T_2+G=0,T_1=-\cos37^\circ|T|i+\sin37^\circ|T|j,T_2=\cos37^\circ|T|i+\sin37^\circ|T|j,联立解得|G|=50\cdot\sin37^\circN.
5. 给定平面多边形,其顶点为P_1(1, 2),P_2(3, 1),P_3(7, 0),P_4(8, 2),
P_5(6, 3),P_6(7, 4),以及P_7(5, 5),求多边形面积.
- 注意到S=\frac{1}{2}|\sum \det(P_i, P_{i+1})|=\frac{37}{2}.
6. 给定一个平面有界闭区域,其边界曲线为\frac{x^2}{9}+\frac{y^2}{16}=1,求区域面积.
- S=\frac{1}{2}|\lim_{n\rightarrow\infty}\sum_{k=0}^{n}\det((3\cos\frac{2\pi k}{n},4\sin\frac{2\pi k}{n}),(3\cos\frac{2(k+1)\pi}{n},4\sin\frac{2(k+1)\pi}{n}))|=|\sum_{k=0}^\infty12\sin\frac{2\pi}{n}|/2=12\pi.
7. 判断下列各组向量是否相互垂直,平行,或二者都不是.
(1) a = (−5, 3, 7),b = (6, −8, 2).
- 都不是.
(2) a = (4, 6),b = (−3, 2).
- 垂直.
(3) a = −i + 2j + 5k,b = 3i + 4j − k.
- 垂直.
(4) a = 2i + 6j − 4k,b = −3i − 9j + 6k.
- 平行.
8. 如下图,甲烷的分子有四个氢原子H环绕着一个碳原子C形成正四面体,并且碳原子居于四面体的中心. 证明H−C−H的夹角是109.5^\circ.
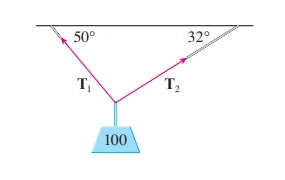
- 由对称性,不妨设H_1(1,0,0),H_2(0,1,0),H_3(0,0,1),H_4(k,k,k),C(t,t,t),由|\overrightarrow{H_1H_2}|=|\overrightarrow{H_1H_4}|解得k=1,由|\overrightarrow{H_1C}|=|\overrightarrow{CH_4}|解得t=\frac{1}{2},因此H-C-H的夹角为\operatorname{Arg}(\overrightarrow{CH_1},\overrightarrow{CH_4})=\arccos(-\frac{1}{3})\approx109.5^\circ.
9. 求v = (1, 2, 3)到u = (3, 6, −1)的数量投影以及投影向量.
- \operatorname{Comp}_uv=\frac{|u\cdot v|}{|u|}=\frac{12}{\sqrt{46}};\operatorname{Proj}_uv=\frac{u\cdot v}{|u|^2}u=\frac{6}{23}(3,6,-1)=(\frac{18}{23},\frac{36}{23},-\frac{6}{23}).
10. 给定平面上三个点P(x_1, y_1),Q(x_2, y_2),及R(x_3, y_3),证明三角形\triangle PQR的有向面积为A(\triangle PQR) =\frac{1}{2}\cdot\begin{vmatrix}1&1 &1 \\x_1 & x_2 & x_3\\y_1 &y_2 &y_3\end{vmatrix},并求P(1, 2),Q(2, 4),及R(5, 6)形成的三角形\triangle PQR的面积.
- 由几何意义有A(\triangle PQR)=\frac{1}{2}\det(\overrightarrow{PQ},\overrightarrow{PR})=\frac{1}{2}\cdot\begin{vmatrix}x_2-x_1&x_3-x_1\\y_2-y_1&y_3-y_1\end{vmatrix}=\frac{1}{2}\cdot\begin{vmatrix}1&0&0\\x_1&x_2-x_1&x_3-x_1\\y_1&y_2-y_1&y_3-y_1\end{vmatrix}=\frac{1}{2}\cdot\begin{vmatrix}1&1 &1 \\x_1 & x_2 & x_3\\y_1 &y_2 &y_3\end{vmatrix},因此S_{\triangle PQR}=|A(\triangle PQR)|=|\frac{1}{2}\cdot\begin{vmatrix}1&1 &1 \\1 & 2 & 5\\2 &4 &6\end{vmatrix}|=2.
11. 给定空间三点P(1, 2, 1),Q(2, 4, −1),及R(5, 6, −3).
(1) 求\triangle PQR的面积.
- S_{\triangle PQR}=|\frac{1}{2}\det(\overrightarrow{PQ},\overrightarrow{PR})|=|\frac{1}{2}\cdot(1,2,-2)\times(4,4,-4)|=2\sqrt2.
(2) 求包含\triangle PQR的平面的法向量.
- \overrightarrow{PQ}\times\overrightarrow{PR}=(1,2,-2)\times(4,4,-4)=(0,-4,-4).
(3) 给出包含P,Q,及R三点的平面的方程.
- ((x,y,z)-(1,2,1))\cdot(0,-4,-4)=0\Rightarrow y+z=3.
12. 给定空间四点P(1, 2, 0),Q(2, 4, −1),R(5, 6, −3),及S(1, 1, 1).
(1) 求以P,Q,R及S为顶点的平行六面体的体积.
- V=|(\overrightarrow{PQ},\overrightarrow{PR},\overrightarrow{PS})|=|((1,2,-1)\times(4,4,-3))\cdot(0,-1,1)|=3.
(2) 求平行六面体相对于包含\triangle PQR的底面的高.
- h=V/(2S_{\triangle PQR})=V/(|\overrightarrow{PQ}\times\overrightarrow{PR}|)=\frac{3}{\sqrt{21}}.
(3) 构造以Q点为坐标原点,以\overrightarrow{QP}为一个坐标轴的右手直角坐标系.
- 注意到\overrightarrow{QP}=(-1,-2,1),(1,0,1)和(-1,1,1)构成右手直角坐标系,即为所求.
13. 给定向量u = (1, 1, 1),v = (1, −1, 1),及w = (3, 5, 7).
(1) 给出包含u及v的子空间W = \operatorname{Span}\{u, v\}的表达式.
- W=\{(m+n,m-n,m+n)|m,n\in\R\}.
(2) 给出w向W投影的正规方程,求投影矩阵R并求\operatorname{Proj}_Ww.
- 记A=[u,v],则正规方程A'Ax=A'w\Rightarrow\begin{bmatrix}3&1\\1&3\end{bmatrix}x=\begin{bmatrix}15\\5\end{bmatrix},因此R=A(A'A)^{-1}A'=\begin{bmatrix}\frac{1}{2} & 0&\frac{1}{2}\\0&1 &0\\\frac{1}{2}&0&\frac{1}{2}\end{bmatrix},\operatorname{Proj}_Ww=Rw=(5,5,5).
(3) 求 w 关于 W 的外投影.
- w-\operatorname{Proj}_Ww=(-2,0,2).




Comments NOTHING